Continuación – Transferencia de masa Gas-líquido

La última ecuación de nuestro post anterior, k_La es una función del volumen de llenado V_L, la frecuencia de agitación n, el diámetro de agitación d₀y el diámetro del matraz d. Los valores dek_Lacalculados muestran una precisión de ± 30%en comparación con los resultados experimentales, que se encuentran en el mismo rango de precisión que las correlaciones de transferencia de masa para biorreactores de tanque agitado. Para las placas de microtitulación, se encontró una correlación adimensional para predecir los valores de k_La:

donde Des el coeficiente de difusión de las especies de difusión en un medio, a_iel área de superficie específica inicial, Re el número de Reynolds, Sc el número de Schmidt (relación entre la difusividad del momento (viscosidad) y la difusividad de la masa), Fr el número de Froude (la relación entre fuerzas inerciales y gravitacionales), y Bo el número de enlace (relación entre las fuerzas gravitacionales y de superficie). En la ecuación se consideran tanto las fuerzas de inercia axial (debido a la agitación) como las fuerzas de superficie (debido a las propiedades del líquido). (Ecuación anterior) por el número de Froude y Bond. Los exponentes x y y en la ecuación anterior depende de la geometría de la placa de microtitulació. Valores calculados a partir de la ecuación se han correlacionado con los valores de k_Lamedidos de los cultivos de Bacillus subtilis en medio mineral y concuerdan dentro de ± 30%. Además, los resultados se compararon con los valores de k_Lamedidos de Hermann. Que también concuerdan bien.

Si se considera la distribución del líquido en las placas de microtitulación, se debe tener en cuenta la tensión superficial del líquido. En tamaños de vasos pequeños, la tensión de la superficie del líquido dificulta la rotación del líquido. Deutz indica que se puede observar la influencia de la tensión superficial de las soluciones acuosas para tamaños de vasos pequeños con un diámetro de pozo <12 mm. Para diámetros de pozo de <4 mm, casi no se observó movimiento de líquido a una frecuencia de agitación de 300 rpm y un diámetro de agitación de 50 mm. Si la tensión superficial no es despreciable, se debe exceder una frecuencia de agitación crítica n_critpara iniciar la rotación del líquido dentro del recipiente. Esta frecuencia de agitación crítica se puede calcular de la siguiente manera:

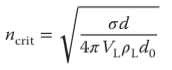
donde 𝜎es la tensión superficial del líquido, d el diámetro del pozo, V_Lel volumen de llenado, 𝜌_Lla densidad del líquido yd₀el diámetro de agitación. Si se excede n_crit, la capacidad máxima de transferencia de oxígeno OTR_maxaumenta al aumentar la frecuencia de agitación. En las frecuencias de agitación por debajo de ncrit, el OTR_maxes independiente de la frecuencia de agitación y alcanza valores al nivel de la transferencia de oxígeno difusivo al líquido estancado no agitado. La tensión superficial 𝜎en la ecuación previa. Depende de las propiedades del líquido. Durante el cultivo, la tensión superficial del líquido se reduce por fragmentos de membrana celular, proteínas, biosurfactantes o glicolípidos extracelulares.

Además de elegir las condiciones de operación apropiadas y las propiedades de la superficie del biorreactor, la integración de deflectores dentro del microbiorreactor representa una alternativa adicional para aumentar la transferencia de oxígeno en biorreactores sacudidos. Incluso si la reproducibilidad de la transferencia de oxígeno entre biorreactores desconcertados individuales es pobre, los deflectores son útiles si la transferencia de oxígeno alta es obligatoria. Funke y otros investigadores informaron un aumento de cinco a diez veces del OTRmax en las placas de microtitulación desconcertadas. Sobre la base de estos datos experimentales, Lattermann publicó una correlación empírica para calcular las capacidades máximas de transferencia de oxígeno en placas de microtitulación de 48 pocillos desconcertados. En esta correlación, el perímetro relativo del pozo Peri se introdujo como parámetro clave. La transferencia de oxígeno se puede calcular en función del perímetro relativo Peri, la frecuencia de agitación n y el volumen de llenado V_L:

En esta ecuación es válido para perímetros relativos <1.1. La aplicabilidad de la ecuación para otros sistemas de biorreactores agitados, como un matraz de agitación, todavía tiene que verificarse. Para calcular el área de transferencia de masa a biorreactores desconcertados, los modelos descritos anteriormente de Büchs y Klöckner no se puede aplicar. Debido a la caótica distribución de líquido indefinida, se deben aplicar simulaciones de CDF para determinar la superficie del líquido en biorreactores agitados desconcertados. Recientemente, Li realizó un análisis de CFD para calcular las áreas de transferencia de masa en matraces de agitación desconcertados para líquidos de viscosidades similares al agua.

Las correlaciones k_Laempíricas en las ecuaciones consideran experimentos con diferentes propiedades líquidas, por ejemplo, el sistema químico de sulfito y los caldos de cultivo. Por lo tanto, los valores de k_Lareportados no pueden compararse directamente entre sí. En general, los valores de OTR_maxdeterminados experimentalmente dependen de la solubilidad del oxígeno en el líquido L_O2y del coeficiente de difusión de oxígeno D en el líquido. Como consecuencia, los valores de k_Laque se han obtenido para un líquido específico deben corregirse con un factor de corrección si se aplican otros líquidos.