biorreactor giratorio de tambor II

Continuando con el modelo giratorio de tambor que vimos en nuestro artículo anterior dentro de estas ecuaciones de balance de energía, hay varios coeficientes de transferencia de calor y masa. El coeficiente de transferencia de calor de la cama a la pared (h_bw) se calcula usando:

Antes de calcular los otros coeficientes de transferencia de calor, el valor de la tasa de flujo de aire en vvm (volúmenes de aire por volumen de biorreactor total por minuto) se usa para calcular la tasa de flujo de aire, F (kg-aire seco s^-1).

Este y el área de sección transversal del espacio de cabeza normal al flujo de gas (A_g, m²) se utilizan para calcular los dos coeficientes de transferencia de calor que implican los gases del espacio de cabeza (W m^-2 ° C^-1), es decir, el espacio entre cama y cabeza coeficiente (h_bh) y el coeficiente espacio de cabeza a pared (h_hw).

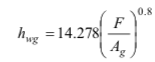
La relación psicrométrica se usa luego para calcular el coeficiente de transferencia de masa del lecho al espacio de cabeza:

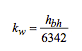
Tenga en cuenta que el denominador también contiene un factor de conversión debido a las unidades utilizadas para la fuerza impulsora en el término que describe la evaporación. Esta ecuación usa h_bh en W m^-2 ° C^-1 y da k_w en kg-H₂O s^-1 m^-2 (kg-H₂O kg-sólidos secos^-1) ^-1. Tenga en cuenta que las unidades entre paréntesis son las unidades de la fuerza motriz. Después de la simplificación, las unidades de k_w son kg-sólidos secos s^-1 m^-2.

Tenga en cuenta que la fuerza motriz para la evaporación es la diferencia entre el contenido de agua de los sólidos (W, kg-H₂O kg- sólidos secos^-1) y el contenido de agua que tendrían los sólidos si estuvieran en equilibrio con el gas en la fase del espacio de cabeza (W_sat).

W_sat se calcula usando la ecuación

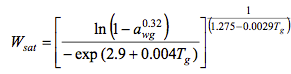
En este caso, la ecuación usa la temperatura del espacio de cabeza y la actividad del agua, esta última calculada como se explica en ecuación

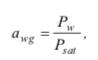
Los valores de los coeficientes de transferencia h_bh y k_w calculados como se describe en el párrafo anterior son para un tambor que no está mezclado. La mezcla debería aumentar el calor de la cama al espacio de cabeza y la transferencia de masa. Sin embargo, no hay suficiente información disponible para incorporar esto de forma mecánica dentro de la ecuación. Por lo tanto, en este modelo, h_bh y k_w simplemente se multiplican por un factor empírico «n», que representa el aumento de veces en las tasas de transferencia debido a la mezcla.

El modelo incorpora dos esquemas de control simples, un control de la humedad del aire de entrada y un control de la actividad del agua de la cama. El control de la humedad del aire de entrada es deseable ya que, aunque el uso de aire seco para promover la evaporación es una estrategia efectiva de enfriamiento, si se usa aire seco al comienzo de la fermentación cuando la tasa de producción de calor metabólico es baja, entonces la temperatura del lecho puede caer a valores lo suficientemente bajos como para retrasar el crecimiento temprano. Por lo tanto, la temperatura de la cama se controla cada hora. Si es menor que la temperatura óptima para el crecimiento (38 ° C), entonces se suministra aire de alta humedad al biorreactor, mientras que si excede esta temperatura, se suministra aire de baja humedad.

La promoción de la evaporación mediante el suministro de aire de baja humedad podría potencialmente secar las actividades de la cama al agua lo suficientemente bajas como para restringir el crecimiento. Por lo tanto, se supone que las muestras se retiran de la cama cada hora y se determina rápidamente su actividad de agua. Si la actividad del agua cae por debajo de un punto establecido, entonces se agrega suficiente agua a la cama para llevar la actividad del agua al valor inicial. Tenga en cuenta que se supone que el agua añadida está a la temperatura de los sólidos y, por lo tanto, no afecta la temperatura de la cama.

Las ecuaciones del modelo son ecuaciones diferenciales ordinarias, ya que el tiempo es la única variable independiente. Se resuelven usando el algoritmo de integración numérica Runge-Kutta.

Predicciones sobre la operación a escala de laboratorio

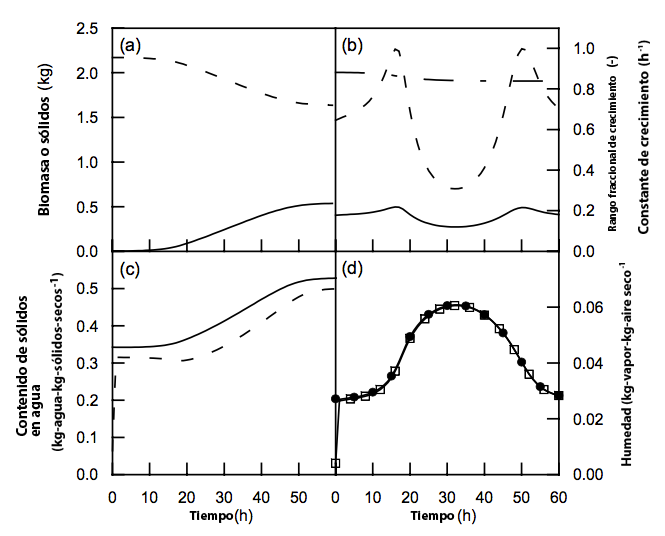
La Figura 23.4 muestra el tipo de información que se puede obtener del modelo.  La salida se puede trazar para ver variaciones temporales en:

• El crecimiento de la biomasa y la disminución de la masa total de sólidos secos (a).
• El valor del parámetro de tasa de crecimiento específico () en la ecuación logística y los efectos relativos de la temperatura y la actividad del agua en el valor de este parámetro (b). En este caso, la temperatura tiene una mayor influencia en el valor de este parámetro.
• La fuerza motriz para la evaporación (c).
• El grado de saturación del espacio de cabeza (d). En este caso, la cabeza el espacio permanece saturado durante toda la fermentación.