El enfoque Euler en biorreactores se supone que todas las fases están en el marco euleriano, es decir, se supone que el marco de referencia es estacionario y que el fluido pasa a través del volumen de control, y las ecuaciones que gobiernan, como el balance de cantidad de movimiento, el balance de masa y calor son resuelto para el fluido que fluye que es fase continua.
Todas las fases se tratan como un continuo separado y comparten el mismo dominio.
Como se mencionó anteriormente, este enfoque se prefiere para los casos en los que la fracción de volumen de la fase dispersa es superior al 10 %.
Los ejemplos en los que se prefiere este enfoque incluyen el modelado de lecho fluidizado, reactor agitado multifásico y reactores de columna de burbujeo.
Como las fases también pueden interpenetrarse entre sí, estas interacciones deben tenerse en cuenta y esto se logra utilizando el término de intercambio de momento de interfase.
Además, el promedio de las ecuaciones gobernantes se realiza por unidad de volumen con la suposición
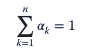
donde 𝛼k es la fracción de volumen de una fase particular y “n” es el número total de fases. La ecuación de continuidad entonces se convierte en
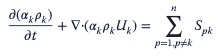
donde 𝜌k es la densidad, Uk es la velocidad media de la fase «k» y Spk es la tasa de transferencia de masa entre las fases «p» y «k». Entonces, la ecuación de la cantidad de movimiento se puede escribir como
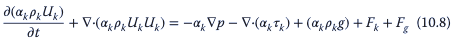
donde Fk es el término de intercambio de impulso de interfase entre la fase «k» y todas las demás fases. Cabe señalar que en el enfoque Euler en biorreactores la presión es común para todas las fases y, por lo tanto, no tiene ningún subíndice en la ecuación con el enfoque Euler en biorreactores. El término de intercambio de impulso de interfase es responsable de todas las interacciones mencionadas anteriormente entre las fases y es un diferenciador clave entre los flujos multifásicos y monofásicos.
En este enfoque, todas las fases se modelan en el marco euleriano y, por lo tanto, el modelado implica resolver las ecuaciones de continuidad, cantidad de movimiento y transporte de masa y energía simultáneamente para todas las fases.
En el caso de sistemas de dos fases, la fase dispersa (como burbujas o gotas) está separada de la fase continua por un límite.
Este límite representa una geometría sólida a través de la cual fluye el fluido y ejecuta movimiento bajo la influencia del flujo a su alrededor.
Cuando la interfaz no es estacionaria, la aplicación de una condición de contorno se vuelve difícil.
Por lo tanto, las ecuaciones se resuelven para todas las fases y se captura el movimiento de todas las fases, capturando así indirectamente el movimiento de la interfaz.
VOF se utiliza principalmente para simular las propiedades interfaciales, como la adhesión a la pared y la tensión superficial.
Este enfoque es útil para modelar solo unas pocas partículas de fase dispersa porque requiere recursos computacionales significativamente grandes.
Dado que todos los fluidos comparten un solo conjunto de ecuaciones, el modelo se puede expresar como
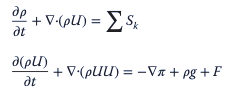
El método de seguimiento frontal se usa para resolver estas ecuaciones numéricamente y es engorroso desde el punto de vista computacional.
Dado que un volumen de control contiene más de un fluido, las ecuaciones mencionadas anteriormente se resuelven utilizando las propiedades de la mezcla.
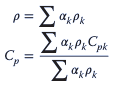
donde 𝛼k es la fracción volumétrica de la fase “k” en el volumen de control. El valor de la fracción de volumen se calcula resolviendo la ecuación de continuidad de la fracción de volumen para N−1 fases.
Debe destacarse que la fracción de volumen no puede determinar la interfaz exacta, ya que diferentes configuraciones de interfaz pueden conducir a las mismas fracciones de volumen.
Por lo tanto, se aplican varias técnicas diferentes para calcular la interfaz exacta.
Hinze ha definido el flujo turbulento como «una condición irregular de flujo en la que varias cantidades muestran una variación aleatoria con las coordenadas de tiempo y espacio, de modo que se pueden discernir valores promedio estadísticamente distintos».
Se observa en el fluido que fluye a medida que aumenta el número de Reynolds.
El cizallamiento es la principal fuente de energía que introduce turbulencia en el flujo laminar.
Por lo tanto, se puede afirmar que si se reduce el corte, el flujo turbulento también se reduciría a laminar y el número de Reynolds disminuiría.
Hasta ahora, no se ha modelado la transición de flujo laminar a turbulento.
Las teorías existentes pueden predecir la transición para pequeñas perturbaciones, pero no para grandes perturbaciones.
Todas estas teorías funcionan bien con un número de Reynolds alto, pero no funcionan con un número de Reynolds bajo.
La ecuación de Navier-Stokes no se puede aplicar directamente a los flujos turbulentos, ya que el flujo es muy complejo para determinar la dinámica de fluidos en cada punto.
Por lo tanto, es necesario agregar nuevos términos a estas ecuaciones para dar cuenta de las fluctuaciones causadas por la turbulencia.
Si se promedian estas ecuaciones en el espacio o el tiempo, entonces el flujo se puede analizar en mayor medida.
Así, para resolver el flujo turbulento en tanques de acero inoxidable, la variable instantánea (velocidad, temperatura, etc.) se divide en dos partes: la variable media y la variable de fluctuación.
Las variables medias se pueden determinar experimentalmente y las variables de fluctuación se pueden modelar para lograr una visualización completa del flujo.
El modelado de las fluctuaciones requiere la conversión de las fluctuaciones desconocidas en variables conocidas que puedan evaluarse fácilmente.
Estas ecuaciones se promedian a lo largo del tiempo. Este método se llama promedio de Reynolds.
La fenomenología de la cascada de energía de Richardson-Kolmogorov-Taylor dice que la turbulencia contiene remolinos de varios tamaños.
Los remolinos grandes son inestables, por lo que se rompen y dan energía a los remolinos más pequeños.
Este proceso continúa hasta que la energía se disipa en forma de disipación viscosa.

