La definición de una fase en biorreactores se puede establecer como el estado termodinámico en el que existe cualquier componente.
Por lo tanto, los flujos multifásicos se refieren a flujos cuando está presente más de una fase en biorreactores.
La mayoría de los reactores industriales tienen procesos de flujo multifásico.
En tales casos, incluso pequeños cambios en el diseño del reactor pueden dar como resultado grandes cambios en la hidrodinámica del reactor.
Los flujos multifásicos se pueden clasificar en varias categorías según la termodinámica (p. ej., gas-sólido, gas-líquido, líquido-líquido) o según los regímenes de flujo.
Ejemplos de estos últimos incluyen flujo disperso en el que solo una fase es continua mientras que todas las demás están dispersas, flujos multifásicos como el flujo de burbujas de gas en líquido, partículas sólidas en líquido o gas y gotitas de líquido en gas, flujos separados en los que todas las fases son de modo semicontinuo y tienen interfaces para diferenciarlos como el flujo anular y el flujo en chorro, y finalmente, los flujos mixtos en los que están presentes tanto los flujos separados como los dispersos, algunas fases son discretas y otras son semicontinuas como el flujo anular burbujeante y flujo anular de gotas.
El modelado CFD de flujo multifásico implica la definición de un régimen de fase/flujo, la formulación de las ecuaciones de gobierno y, finalmente, la solución de las ecuaciones de gobierno. Los enfoques que se utilizan comúnmente incluyen.
1) Enfoque Euleriano – Lagrangiano que implica la aplicación del enfoque Euleriano para la fase en biorreactores continua y el marco Lagrangiano para la fase dispersa.
2) Euleriano: enfoque euleriano que implica la aplicación del enfoque euleriano para ambas fases sin tener en cuenta explícitamente la interfaz
3) enfoque de volumen de fluido que implica la aplicación del marco Euleriano para ambas fases con reforma de la interfaz en base al volumen.
Enfoque Euleriano-Lagrangiano
Se prefiere este enfoque cuando el objetivo es modelar el movimiento de partículas, incluidas las colisiones de traslación, rotación y partícula-partícula que ocurren en procesos tales como reacciones químicas o transferencia de calor y masa entre la fase dispersa y la fase en biorreactores gaseosa a escala de partículas individuales.
En el enfoque Euleriano-Lagrangiano, la fase dispersa se simula resolviendo la ecuación de movimiento mientras que la fase continua se simula resolviendo la ecuación de Navier-Stokes.
La ecuación de movimiento para una sola partícula en fase dispersa se escribe como
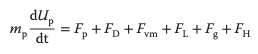
donde mp y Up son la masa y la velocidad media de la partícula, respectivamente.
El lado derecho de la ecuación representa la suma de todas las fuerzas que actúan sobre la partícula, mientras que el lado izquierdo de la ecuación denota la tasa de cambio del momento.
La fuerza, Fp, es la fuerza del gradiente de presión de fase continua y Fg es la fuerza gravitatoria que actúa sobre la partícula. Ambas fuerzas pueden combinarse y escribirse como
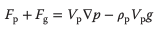
donde Vp es el volumen de la partícula y p es la presión de la fase continua.
La fuerza de arrastre en la partícula debido a la velocidad relativa entre la fase continua y la fase dispersa, FD, en el número de Reynolds más alto, se puede indicar como
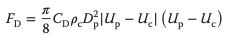
donde el subíndice “c” denota la fase continua y “p” denota la fase de partículas. CD es el coeficiente de arrastre y depende del régimen de flujo si el flujo es laminar o turbulento y su valor cambia en consecuencia.
Otras fuerzas que se pueden incluir son la fuerza de sustentación, las fuerzas de masa añadida y las fuerzas de Basset que actúan sobre la partícula. La vorticidad o cizallamiento en la fase continua también aplica fuerza sobre la partícula de la fase dispersa.
Esta fuerza está incluida en la fuerza de sustentación. Cuando la fase dispersa se mueve hacia arriba, se lleva consigo una parte de la fase continua.
Esto se suma a la masa de las partículas de la fase dispersa.
Como la fase dispersa y la fase continua no pueden ocupar el mismo espacio físico simultáneamente, la masa agregada se modela como un volumen de fluido que se mueve con el objeto por simplicidad matemática.
Esta masa adicional a la fase dispersa contribuye a la «fuerza de masa virtual» o «fuerza de masa añadida».
Otras fuerzas que pueden desempeñar un papel incluyen las fuerzas de Basset que explican los efectos viscosos y el retraso en el desarrollo de la capa límite a medida que la velocidad relativa cambia con el tiempo.
Sin embargo, la magnitud es muy inferior en comparación con las fuerzas de arrastre, por lo que a menudo se ignoran durante la simulación.
Las fuerzas principales que deben tenerse en cuenta incluyen la fuerza de arrastre y la fuerza de presión que actúan sobre la fase dispersa.
Para resolver el flujo de la fase continua, se requiere la velocidad de la fase continua.
Este último se puede calcular resolviendo simultáneamente la ecuación de continuidad y la ecuación de Navier-Stokes para la fase continua
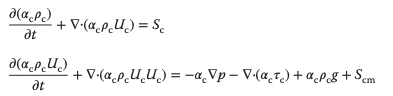
donde Sc y Scm son los términos fuente para la masa y el momento, respectivamente.
Estos términos representan el intercambio entre la fase continua y la fase dispersa.
Cuando la fracción de volumen de la fase dispersa es demasiado baja, se puede ignorar el efecto de la fase dispersa en la fase continua, reduciendo así las ecuaciones de la fase continua a las de la fase única.
La interacción entre la fase dispersa y la fase continua depende del grado de acoplamiento entre las fases.
El acoplamiento puede ser unidireccional cuando la fracción de volumen de la fase dispersa es demasiado baja y entonces se puede suponer que no afectará a la fase continua pero sí a la fase continua.
En un acoplamiento bidireccional, la fase dispersa afecta a la fase continua y viceversa, mientras que en un acoplamiento cuádruple también se tienen en cuenta las interacciones partícula-partícula.
A medida que aumenta el número de partículas a simular, el tiempo computacional requerido para realizar la simulación siguiendo el enfoque Euleriano-Lagrangiano también aumenta y, por lo tanto, el uso de este enfoque generalmente se limita a los casos en que la fracción de volumen de la fase dispersa no excede el 10%.
Para los casos donde la fracción de volumen de la fase dispersa es más alta o para los casos donde las interacciones partícula-partícula de la fase dispersa son fuertes, el enfoque de Euler-Euler es más eficiente y se analiza en la siguiente sección.

