El objetivo del estudio de Modelado Numérico de Flujo Gas-Líquido fue crear un modelo para el flujo de gas-líquido en un biorreactor de tanque agitado utilizando el modelo Euleriano de dos fluidos que es independiente de los datos empíricos, para predecir la retención de gas, el tamaño de las burbujas y los patrones de flujo en los reactores agitados por una turbina y un impulsor.
Se utilizó un enfoque Euleriano-Euleriano en el modelo Flujo Gas-Líquido para resolver las ecuaciones de gobierno para las fases gaseosa y líquida.
Se supuso que el término de intercambio de cantidad de movimiento de la interfaz era un efecto combinado de la fuerza de arrastre, la fuerza de masa añadida, la fuerza de sustentación y la fuerza de dispersión turbulenta.
Dado que la resistencia depende de la turbulencia en el modelo Flujo Gas-Líquido, se propuso la siguiente correlación:
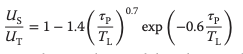
donde US y UT son la velocidad real de deslizamiento y la velocidad terminal estancada, respectivamente; y τP y TL son el tiempo de relajación de la burbuja y la escala de tiempo turbulento, respectivamente.
Se aplicó el modelo estándar k–𝜀 para la turbulencia.
Se añadió un término adicional a la expresión de la viscosidad turbulenta para tener en cuenta la velocidad de deslizamiento de las burbujas.
La fase gaseosa también se consideró de naturaleza turbulenta.
En lugar de considerar la distribución completa del tamaño de la burbuja, lo que aumenta el uso de recursos informáticos, se utilizó el modelo para predecir el diámetro medio de la burbuja en el reactor en función de la densidad numérica de la burbuja.
El modelo se da de la siguiente manera:
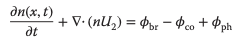
donde 𝜑br, 𝜑co y 𝜑ph son las tasas de ruptura, coalescencia y cambio de fase, respectivamente.
Los autores del estudio del modelo Flujo Gas-Líquido modelaron la formación de la cavidad de gas ventilada cerca de las palas del impulsor, donde las burbujas de gas no se comportan como una fase dispersa.
Se hicieron modificaciones en las ecuaciones gobernantes para incorporar estas condiciones en el mismo marco Euleriano.
Las condiciones de operación se mantuvieron similares a las de las condiciones de operación experimentales.
Con la turbina, solo se modeló una sección de 60 ∘ del tanque, incluyendo un deflector y un álabe del impulsor, y se aplicó la condición de frontera periódica (la dinámica de flujo en esta sección del reactor se repitió en secciones posteriores).
Se utilizaron alrededor de 59 000 celdas para la simulación de esta sección.
Se utilizó un modelo de marco de referencia múltiple (MRF) para modelar un marco giratorio para la región del impulsor.
Para el impulsor Lightnin, era necesario simular el reactor completo debido al diseño del impulsor y, por lo tanto, se utilizaron 183 000 celdas.
El método MRF no dio resultados estables para el último impulsor y, por lo tanto, se utilizó el método de malla deslizante.
Se realizaron cuatro simulaciones diferentes con la turbina Rushton cambiando el caudal de entrada de gas y la velocidad de rotación del impulsor.
Se compararon los resultados obtenidos con el método estándar (como se menciona en el código CFX) y los modelos mejorados de dispersión turbulenta y arrastre sugeridos por los autores, y se vio que los modelos sugeridos por los autores produjeron resultados más cercanos a los resultados experimentales.
Se observa que las burbujas de gas se acumulan en la región debajo del impulsor.
Al aumentar el caudal, aumenta la acumulación.
Los autores también compararon modelos estándar y modificados, y se concluyó que los modelos estándar subestimaron los valores de fracción de volumen de gas, especialmente en la región superior.
Por lo tanto, los autores modelaron con éxito el flujo gas-líquido y mejoraron los modelos publicados anteriormente, mejorando así la capacidad predictiva del modelo.
Se creó un nuevo modelo para predecir el coeficiente de arrastre para tener en cuenta las interacciones entre la burbuja y el remolino.
Se utilizó un rango de condiciones de operación para la simulación del reactor.
Los resultados simulados estaban en buen acuerdo con los resultados experimentales de retención de gas, distribución del tamaño de burbuja y fracción de volumen de gas.
CFD está encontrando cada vez más aplicaciones en bioprocesamiento, particularmente en el modelado de distribución de flujo en biorreactores.
Se ha convertido en una potente herramienta que se puede utilizar de forma eficaz para comprender los efectos de varios parámetros en las respuestas de salida, reduciendo así la necesidad de realizar experimentos en los reactores a gran escala.
Es evidente que el conocimiento de la hidrodinámica puede ser de gran ayuda para los investigadores que buscan (i) mejorar el diseño del reactor, (ii) optimizar y escalar el proceso y/o (iii) intentar comprender interacciones entre los diversos parámetros de entrada significativos (como la velocidad de agitación, el caudal de gas).
Es probable que el futuro vea una adopción a gran escala de CFD entre los desarrolladores de procesos.

