Paso 5: Resuelva el modelo que creó para el bioreactor

Esta serie de posts no proporcionamos información detallada sobre cómo se resuelven los modelos matemáticos. Normalmente, se utilizarán técnicas numéricas para resolver ecuaciones diferenciales. La cantidad de trabajo que se debe hacer para resolver un modelo depende de la sofisticación del software de computadora disponible. En algunos casos es necesario escribir un programa en un código de computadora como FORTRAN o MatLab, utilizando subrutinas preescritas según corresponda. Con paquetes de software más sofisticados, puede ser suficiente simplemente introducir las ecuaciones y los valores iniciales en los campos apropiados y pedirle a la computadora que resuelva las ecuaciones.
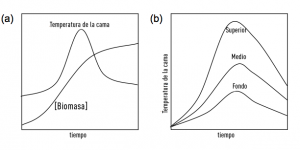
Los sistemas bien mezclados conducirán a un conjunto de ecuaciones diferenciales ordinarias (EDO), es decir, ecuaciones en las que los términos diferenciales sólo se expresan como funciones del tiempo. Tal conjunto de ecuaciones puede ser resuelto con subrutinas bien conocidas, como la subrutina FORTRAN DRKGS, que se basa en el algoritmo de Runge-Kutta. La solución de tales modelos será un gráfico, trazado en función del tiempo, de las variables del sistema que fueron descritas por las ecuaciones diferenciales. En el caso del modelo de biorreactor de SSF bien mezclado, la solución del modelo está representada por perfiles de biomasa temporal y temperatura del lecho, tales como las predicciones presentadas en la imagen siguiente.
Los sistemas con heterogeneidad espacial y temporal conducirán a ecuaciones diferenciales parciales (EDPs), es decir, ecuaciones que contienen una mezcla de términos diferenciales que contienen tiempo en el denominador y términos diferenciales que contienen una coordenada espacial en el denominador. Los métodos de solución implican transformar las PDEs en conjuntos de ODEs, y luego utilizar la integración numérica para resolver estas ODEs. Típicamente la transformación de las PDEs en conjuntos de ODEs se debe hacer a mano, y no es simple de hacer. La solución de tal modelo será un gráfico en función del tiempo de cada una de las variables de estado, con múltiples curvas, representando cada curva una posición diferente dentro del lecho.
Paso 6: validar el modelo
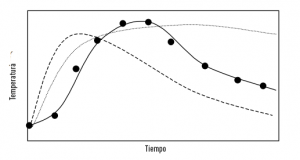
Si se ha resuelto un modelo usando estimaciones independientes de todos los parámetros, entonces es de gran interés si el modelo logra predecir razonablemente bien el comportamiento del sistema que se observa experimentalmente en la figura siguiente. Si lo hace, entonces esto puede tomarse como evidencia de apoyo, pero no como prueba, de que los mecanismos y fenómenos incluidos en el modelo son efectivamente los que son más importantes para determinar el comportamiento del biorreactor. Desafortunadamente, la validación de modelos de biorreactores sólo se ha hecho muy raramente en el área de SSF hasta la fecha.
Como se ha mencionado en el paso 4, en algunos casos se determinan uno o más de los parámetros durante la etapa de solución, realizando varias simulaciones con diferentes valores para estos parámetros y viendo qué solución coincide mejor con los datos experimentales (Esto se hace de manera más eficaz mediante el uso de una rutina de optimización para encontrar el valor del parámetro que da el mejor ajuste estadístico). El peligro de este enfoque es que podría ser posible ajustar el modelo a los datos incluso si los mecanismos incluidos en el modelo son inadecuados. Cuando este enfoque se utiliza para la estimación de parámetros, no es posible afirmar que el modelo ha sido validado, incluso si se obtiene un acuerdo muy estrecho.
Un análisis de sensibilidad podría hacerse en esta etapa. Esto implica hacer cambios uno a la vez a los diversos parámetros en el modelo y ver cuán grande es el efecto en las predicciones del modelo. Esto implica hacer cambios uno a la vez a los diversos parámetros en el modelo y ver cuán grande es el efecto en las predicciones del modelo. El objetivo es determinar qué parámetros son los más importantes para determinar el rendimiento del bioreactor:
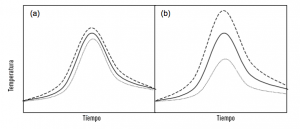
Si cambios relativamente pequeños en el valor de un parámetro afectan significativamente las predicciones del modelo, entonces muy probablemente el fenómeno al que está asociado el parámetro es muy importante para determinar el comportamiento del sistema y, además, es muy importante obtener valores precisos para el parámetro;
Si los cambios relativamente grandes en el valor de un parámetro tienen un efecto relativamente pequeño en las predicciones del modelo, entonces el fenómeno al que se asocia el parámetro no es muy importante para determinar el comportamiento del sistema, al menos en el conjunto particular de condiciones de operación utilizado El fenómeno podría ser más importante bajo otro conjunto de condiciones operativas). El grado de precisión necesario para la estimación de este parámetro no es tan grande y posiblemente el término que describe este parámetro puede eliminarse para simplificar el modelo.

