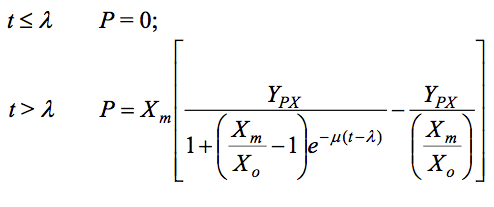Formación de productos – Enfoques empíricos

Dada la dificultad de modelar el crecimiento de la biomasa en sistemas de SSF incluso con ecuaciones empíricas simples, no es sorprendente que se haya prestado mucha atención a superar estas dificultades y que se haya prestado poca atención al modelado de la cinética de la formación del producto. De hecho, puede ser muy difícil utilizar otras ecuaciones empíricas simples para la formación de productos dentro de un modelo de biorreactor, especialmente para productos como enzimas o metabolitos secundarios. De hecho, puede ser muy difícil utilizar otras ecuaciones empíricas simples para la formación de productos dentro de un modelo de biorreactor, especialmente para productos como enzimas o metabolitos secundarios. La producción de estos productos puede depender de variables tales como la tasa de absorción de nutrientes.
Como se argumentó anteriormente la absorción de nutrientes es a menudo controlada por la velocidad a la que el nutriente se difunde a la superficie, y esto sólo puede predecirse mediante un modelo que describa los procesos de difusión intrapartícula. Estos modelos son demasiado complejos para incluir en modelos de biorreactores de resolución rápida. La ecuación empírica de Leudeking y Piret podría ser utilizada:
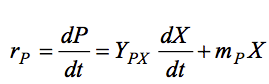
donde rP es la tasa global de formación del producto (kg h-1). YPX es el rendimiento del producto de la reacción de crecimiento (kg-producto kg-biomasa seca-1) y mP es el coeficiente de formación del producto relacionado con el metabolismo de mantenimiento (kg-producto kg-biomasa seca-1 h-1).
Con el fin de determinar los coeficientes de rendimiento y mantenimiento de la ecuación anterior puede ser necesario ajustar una versión integrada de esta ecuación al perfil del producto. Como en ese caso, es necesario sustituir las versiones integral y diferencial de la ecuación cinética en la ecuación.
Por ejemplo, con la cinética de crecimiento logístico, es posible derivar la siguiente ecuación integrada:
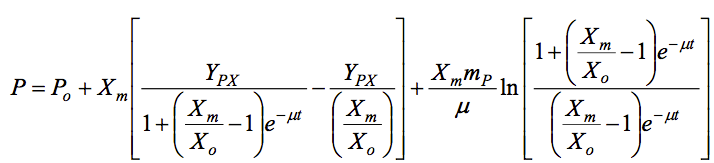
donde Po es el producto presente en el tiempo cero (kg). Como en otras ecuaciones presentadas anteriormente, si Xo, Xm, se determinan a partir del perfil de biomasa, entonces las únicas incógnitas en esta ecuación son mP y YPX, y éstas pueden ser determinadas por un ajuste de mínimos cuadrados de la anterior al perfil del producto.
Ooijkaas y otros utilizaron este enfoque para caracterizar la cinética de producción de esporas, con dos diferencias menores.
En primer lugar, se asumió que la producción de esporas asociada al mantenimiento era cero, lo que significa que el término que implicaba mp desapareció de la ecuación y, en segundo lugar, hubo un retraso en la aparición de las primeras esporas, que se tuvo en cuenta restando la fase de retardo del tiempo de fermentación total.
Además, el número inicial de esporas se tomó como cero. Para un producto que sigue estas condiciones, la ecuación es: