En el Modelo de tensión de Reynolds se calcula las fluctuaciones que ocurren en el flujo y, por lo tanto, permite la visualización del flujo. Las variables en las ecuaciones gobernantes se descomponen en una variable media y una variable fluctuante. El promedio de tiempo o conjunto se realiza en estas ecuaciones. La parte fluctuante tiende a cero ya que el promedio de las fluctuaciones es cero y las ecuaciones se dejan solo en términos de variables medias. La ecuación variable media se resta de la ecuación descompuesta no promediada para obtener la ecuación solo en términos de fluctuaciones. Esta ecuación se multiplica por otros componentes fluctuantes para obtener las ecuaciones del modelo de tensión de Reynolds:
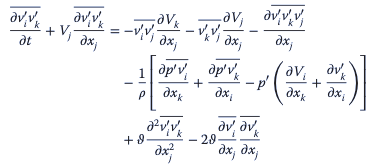
donde v′ representa la velocidad fluctuante, “V ” representa la velocidad media y la barra superior representa el promedio que se realiza a lo largo del tiempo o conjunto. Los términos v′iv′k, v′iv′j y v′kv′j se denominan tensiones de Reynolds. Al resolver estas ecuaciones, se pueden modelar las fluctuaciones y se puede estimar el perfil de flujo.
Modelo k – 𝜺
Este modelo también utiliza un procedimiento similar al modelo de tensión de Reynolds (RSM) para obtener la ecuación en términos de variable fluctuante. La variable fluctuante se transforma en energía cinética turbulenta “k” y tasa de disipación de energía turbulenta “𝜀”. Esta última es la velocidad a la que un remolino grande da energía a los remolinos más pequeños. La ecuación final se puede escribir como
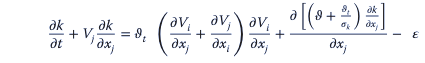
donde 𝜗t es la viscosidad cinemática turbulenta y 𝜎k es la constante empírica.
Img 3
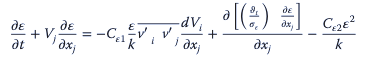
donde C𝜀1, 𝜎𝜀 y C𝜀2 son las constantes empíricas.
El modelo de tensión de Reynolds da mejores resultados que el modelo k–𝜀 ya que resuelve y estima el componente fluctuante directamente, pero tiene el inconveniente de que el número de ecuaciones a resolver es significativamente mayor en comparación con el modelo k–𝜀, lo que resulta en un cálculo engorroso y lento. Aunque existen muchos más modelos para modelar la turbulencia en el flujo, los dos mencionados aquí son los más utilizados.
En los biorreactores típicos de tanque de acero inoxidable, existe una distribución de tamaños para las burbujas dentro del biorreactor.
Esta distribución se produce debido a fenómenos como la nucleación, la agregación y la rotura. La ruptura y la coalescencia de las burbujas ocurren debido a las interacciones con los remolinos turbulentos.
La ruptura ocurre cuando la energía superficial de la burbuja aumenta y alcanza un valor crítico. El aumento de la energía superficial se debe a la interacción con los remolinos turbulentos.
Los remolinos que provocan la ruptura son del mismo tamaño que la burbuja o de menor tamaño. Los remolinos más grandes no provocan roturas; simplemente llevan la burbuja con ellos.
La coalescencia de las burbujas tiene lugar debido a la turbulencia, la flotabilidad y la cizalladura laminar. La coalescencia de las burbujas depende de la frecuencia de colisión y la eficiencia de la colisión.
Por lo tanto, el balance de población debe incorporarse en las ecuaciones de transporte de cantidad de movimiento, masa y energía para tener en cuenta el tamaño cambiante de la fase dispersa.
Dado que la distribución de tamaño determina el área interfacial total disponible, también afecta significativamente la transferencia de masa total entre las fases.
La distribución de burbujas se calcula mediante PBM utilizando las siguientes ecuaciones:
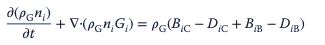
donde BiC y BiB son las tasas de natalidad de las partículas y DiC y DiB son las tasas de muerte de las partículas por coalescencia y rotura, respectivamente.
El subíndice «i» denota la clase de burbuja particular que se está considerando.
Las tasas de natalidad y las tasas de mortalidad se pueden calcular como
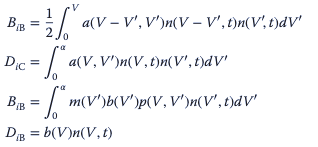
donde a(V,V′) significa la tasa de coalescencia entre burbujas con volúmenes V ′′′′ y V , y (V ) es la tasa de rotura de burbujas con volumen.
El término mm(V) es el número de burbujas hijas formadas debido a la ruptura de burbujas de volumen V′, y n(V,t) es el número de burbujas de volumen V en el tiempo t.
El término p(V,V′) es la función de densidad de probabilidad para burbujas de volumen V generadas a partir de burbujas ′ de volumen V.
La fracción de volumen del tamaño de burbuja 𝛼i, del componente «i», se puede definir como
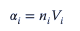
Hay varias formas de resolver las ecuaciones anteriores:
Método discreto: El tamaño de partícula se discretiza en un número finito de intervalos de tamaño, es decir, la fase dispersa puede tener solo tamaños discretos correspondientes a intervalos de tamaño. Este enfoque se puede utilizar para definir directamente la distribución del tamaño de las partículas.
Método discreto no homogéneo: Diferentes grupos de contenedores se mueven a diferentes velocidades. Esta es una mejor representación de lo que realmente ocurre en el reactor (partículas de diferentes tamaños tienen diferentes momentos).
Método estándar de momentos: La ecuación de balance de población (PBE) se transforma en ecuaciones de transporte para los momentos de la distribución. Esto es computacionalmente más simple que el método discreto, pero tiene la limitación de que la agregación y la rotura no están incluidas.
Método de cuadratura de momentos:Este método se puede aplicar a una amplia gama de áreas ya que no sufre las limitaciones del método estándar de momentos.

